采用峰值电流控制的变换器相对于电压控制模式具有更佳的动态特性,但是当其工作在CCM模式下且占空比大于50%时会出现开环不稳定(次谐波震荡)现象,产生机理可从以下两方面分析:
一、通过过程分析
资料中的常见解释,当占空比<0.5扰动逐渐收敛,当占空比>0.5扰动逐渐发散。
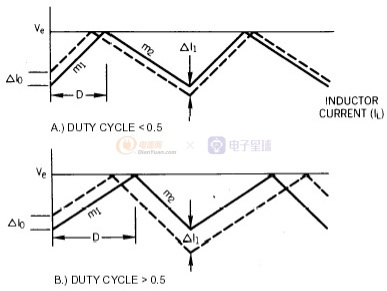
图1-1 通过趋势分析次谐波震荡
二、通过结果分析
次谐波震荡也是一种稳态满足伏秒平衡,所以可以利用最终的稳态结果进行分析。
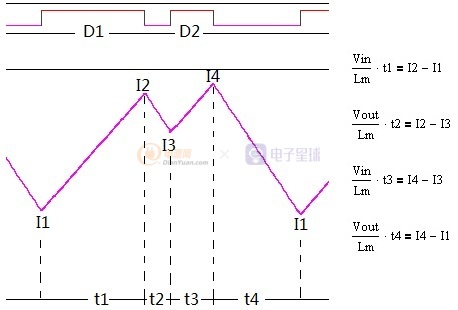
图1-2 稳态下的次谐波震荡电流波形
上图展示了次谐波震荡下的稳态波形既连续两周期满足伏秒平衡,有两个问题需要说明一下:
- 为什么不会发生多个周期的次谐波震荡?
一般电流检测电路要加消隐电路(RC低通)顺便滤掉了高次谐波所以只剩下连续两周期的次谐波震荡(既大小波)。
- 为何占空比<0.5时不会发生次谐波震荡?
因为占空比小于0.5的次谐波震荡在实际电路中不具备发生条件,见下图:
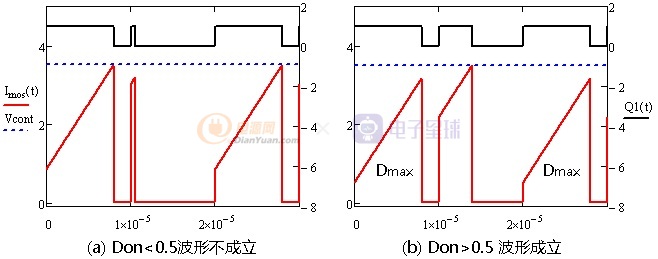
图1-3 真、假次谐波震荡
上图(b)其峰值分别由最大占空Dmax和Vcont控制而图(a)中矮、窄峰是不成立的所以次谐波震荡也是不成立。
通过两周期伏秒平衡公式可以得出大小波的占空比关系:D1+D2=2*Dnorm。
弄清机理之后就可以开始寻找解决方案,要解决的是一个占空比不能大于0.5而又需要大于0.5的矛盾问题(例如电流模式宽输入应用)。
解决方案以下图为示例:

图1-4 斜坡补偿原理
上图1-4中红色为电流波形,正常情况下是要发生次谐波震荡的,如果增加一个斜坡(蓝色虚线)使原来的上升斜率从m1变为m1+m下降斜率从m2变为m2-m且m1+m≥m2-m(变化后的绿色虚线),从控制器的角度看占空比是小于等于0.5的就避免了发生次谐波震荡。(其中m1、m2、m都取正数)
补偿斜坡也可以加在Vcont信号上效果相同,见下图。
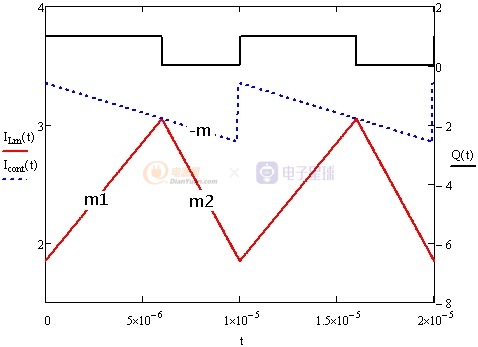
图1-5 补偿斜坡加在Vcont信号上
至此我们得到了最小斜坡补偿参数m≥(m2-m1)/2,而最大斜坡补偿参数为m≤m2。
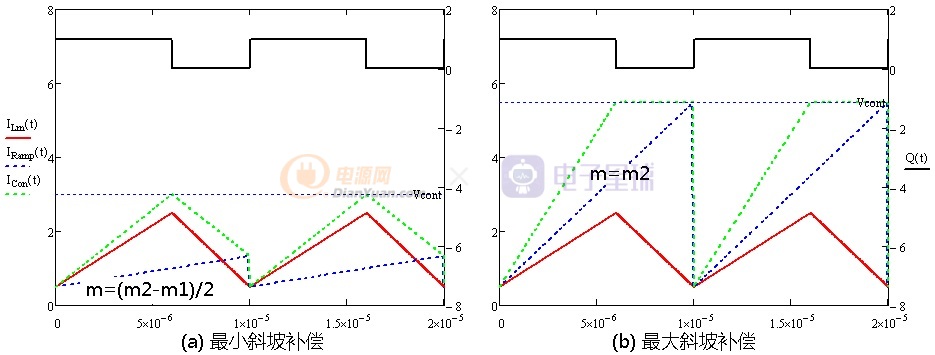
图1-6 最小、最大斜坡补偿波形
通过归一化处理并绘制出反激电路最大、最小斜坡补偿参数与最大占空比的关系如下图:
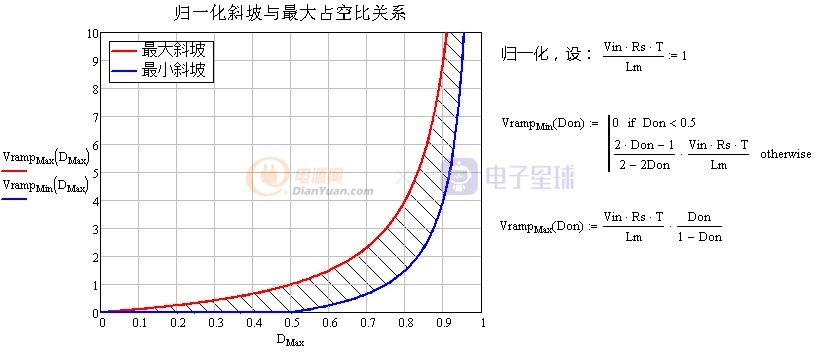
图1-7 反激归一化的斜坡与最大占空比关系
斜坡补偿虽然能够解决CCM峰值电流模式的次谐波震荡问题,但也会带来不利因素使电路特性趋向于电压控制模式。
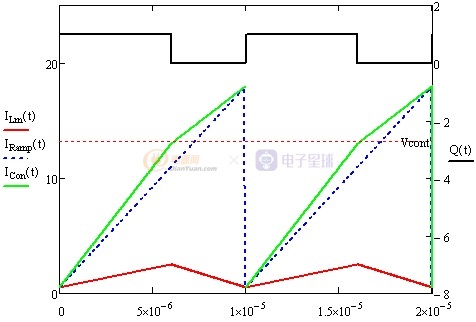
图1-8 过补偿
图1-8显示的是过补偿波形已经近似于电压控制模式这就失去了原电流控制模式的优势,所以补偿应适度。


